
In the last three decades, industries have shifted to a more tech friendly environment. This created a higher demand for programmers, scalable applications, and the ability to improve the applications that consumers and employees use daily. This created a demand for finding better ways to optimize programmable applications and increase performance and productivity. Humans are problem solvers, always trying to devise the best way to find a solution. People complete their task in different ways. Some solutions are effective but take time. While other solutions may be finished quickly, the job is sloppy. The same thing can be said about programming code. The goal is to find both an optimal and time efficient solution that can limit the run time of the application and give the user more time to complete other tasks. An excellent method to complete this goal is dynamic programming.
Dynamic programming is a method created by Richard Bellman in the 1950s. The top tech companies, such as Google, Wal-Mart, and Amazon, all use the dynamic programming method. They even use interview questions to test the knowledge, critical thinking, and analytical skills of their candidates to see how much they understand and comprehend about dynamic programming. This chapter will break down and give a generalization of what dynamic programming is, how it is applied to code, and will break dynamic programming down into three parts: recursion, memoization, and the difference between bottom-up and top-down approach.
Dynamic Programming is mainly an optimization over plain recursion. Recursion is when a program calls back on the same function or variable that has been declared.
#Note how the function calls on itself and we have another call to return recursion(). This is one of the most basic examples of recursion. def recursion(): print("You could not live with your own failure. Where did that bring you? Back to me. --Thanos") return recursion() #recursion() #Removing the comment from above will cause the recursion function to loop infinitely because it will keep calling on itself.

Figure 1: Visual example of recursion
Example 1: Let’s take a look at a real example of recursion.
Let’s try to understand this by taking an example of Fibonacci numbers.
Fibonacci (n) = 1; if n = 0 Fibonacci (n) = 1; if n = 1 Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)
The first few numbers in this series will be: 1, 1, 2, 3, 5, 8, 13, 21… and so on!
A code for the Fibonacci Sequence is using pure recursion:
def fib(n): if n==1 or n==2: return 1 else: fibSeq = fib(n-1) + fib(n-2) return fibSeq
print(fib(1))
print(fib(20))
6765
Time complexity is defined by the amount of time it takes for the program to run.
Space complexity is defined as how much space an algorithm or program takes up.
T(n) = T(n-1) + T(n-2) is exponential. We can observe that this implementation does a lot of repeated work (see the following recursion tree). This is a bad implementation for nth Fibonacci number. Since the Fibonacci method does only a constant amount of work, the time complexity is proportional to the number of calls to Fibonacci Sequence, that is the number of nodes in the recursive call tree.
The recursive call tree is a binary tree, and for fib(n) it has n levels. Therefore, the maximum number of nodes in this tree is 2n−1. The time complexity is thus \(O(2^n)\) .
The Fibonacci Sequence requires just a constant amount of memory, but each recursive call adds a frame to the system’s call stack. Thus, the algorithm uses space proportional to the maximum number of the Fibonacci Sequence frames that can be simultaneously on the call stack. This equals the number of levels of the recursive call tree.
For fib(n), the number of levels of the recursive call tree is n. Thus, the space complexity of the algorithm is \(O(n)\) .
Wherever there is a recursive solution that has repeated calls for certain types of input, we can optimize it using dynamic programming. The idea is to simply store that results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial. Since dynamic programming is optimizing problems by breaking down the algorithm into subproblems, it helps prevent each subproblem from being solved more than once which can be achieved by running a recursive function once and storing in memory this is called memoization.
Memoization prevents continuous solving of the same recursive subproblems by creating a ‘sticky note’ like save-state per inputs to be called for later calculations. This programming technique takes advantage of the CPU’s cache and stores those more time-consuming calculations to later be used when called on throughout the solutions.

Figure 2: Memoization: Recursive calls are stored in an array. With sticky notes, information gets written down and the sticky notes get be placed next to each other. This is the same way an array stores its data in memory.
Memoization should only be used for recursive calculations so that when requesting an output it will stay consistent each time calculations are executed. If not, the program would lose its efficiency and gained advantages as memoization would in the end take up more CPU cycle times to verify its cache stored data in verifying whether the output would be the same or not. Global variables would also greatly influence or break a memoized function. A different algorithm would be much more acceptable.
Example 2: Memoization
Objective: To efficiently calculate a sequence of matrices
Sidenote: Not focusing on the multiplication itself but finding the best route to make the calculations. In some problems, where you put parentheses can either minimize or maximize the number of operations needed to find a solution.
The problem in question:
ABCD = A(BCD) = (AB)(CD) = (AD)(BC) = ALL PRODUCE SAME OUTPUT
A = 10 x 20 B = 20 x 30 C = 30 x 40 D = 40 x 60
Here we would like to demonstrate difference in the number of operations needed when you change up the sequence in which you attempt to calculate the matrices.
(AB)C -> (10 x 20 x 30) + (10 x 30 x 40) = 6000 + 12,000 = 18,000 operations
A(BC) -> (20 x 30 x 40) + (10 x 20 x 40) = 24,000 + 8,000 = 32,000 operations
Calculating (AB)C would take almost half the time of calculating A(BC)
#To show operations needed for certain sequence of matrices import sys def MtxChainOrder(p, n): m = [[0 for x in range(n)] for x in range(n)] for i in range(1, n): m[i][i] = 0 for Lst in range(2, n): for i in range(1, n-Lst + 1): j = i + Lst-1 m[i][j] = sys.maxsize for k in range(i, j): q = m[i][k] + m[k + 1][j] + p[i-1]*p[k]*p[j] if q m[i][j]: m[i][j] = q return m[1][n-1] ele = int(input("Enter how many elements : ")) lst = list(map(int,input("\nEnter Matrices: ").strip().split()))[:ele] size = len(lst) print("\nMinimum number of operations for Matrices entered is " + str(MtxChainOrder(lst, size))) #To represent ideal sequence for most efficient calculation array = [10, 20, 30, 40] size2 = len(array) print("\nMinimum number of operations possible: ", MtxChainOrder(array, size2)) #How to input: #Enter how many elements : #Enter 4 #Enter Matrices: #Enter 10 20 30 40 #Try it with other examples.
Enter how many elements : 4 Enter Matrices: 10 20 30 40
Minimum number of operations for Matrices entered is 18000 Minimum number of operations possible: 18000
Time complexity is \(O(n^3)\) .
Recursion and memoization both take a top-down approach to solving the problem. This means that the problem is looked at as a whole and is broken down into pieces, examining each piece to see how it makes a whole. Top-down can even go further by breaking down the parts into sub subparts. The main languages that also focus on top-down approach are COBOL, Fortran, and C.
Take a look at a plastic model car for example. For top-down we will start by looking at the model car(the root). Because top-down is a decomposition process, we will break the model car down into pieces. You will have many parts: the engine, wheels, the body, and the interior. All these items are separate, but they end up forming the model car. Because they are separate, this can cause redundancy and communication errors within the program.
In most cases, it is better to take a bottom-up approach rather than a top-down approach. Bottom-up has a different approach, it uses composition. Instead of starting from the root, it starts from the bottom, the smallest variable types, and moves upward towards the root. This means that we will build it from the ground up. In the model car example, this would be like pulling the model out of the box. All the pieces are connected, but it still needs to be assembled. The pieces represent the subproblems and the sub subproblems. In objected-oriented programming we can define the model car as a class, meaning that all pieces are no longer separated but in constant communication and reduce redundancy. Good examples for bottom-up are object-oriented languages; languages like C++, C#, and Java, all use the bottom-up approach because the object is always identified first. Finally, once we add each piece and put all the pieces together, we will have a functional model car.
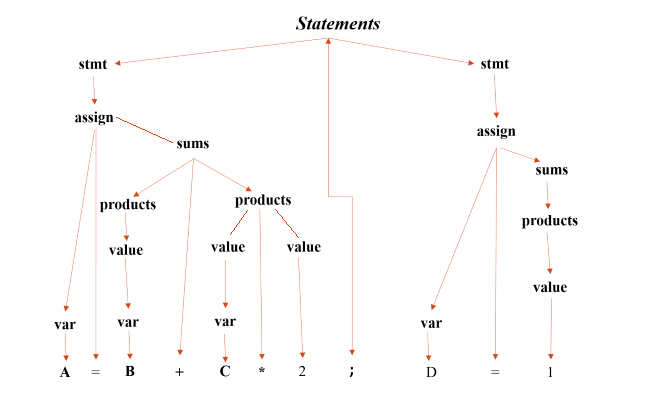
Figure 3: Parse tree with the root called “Statements”.
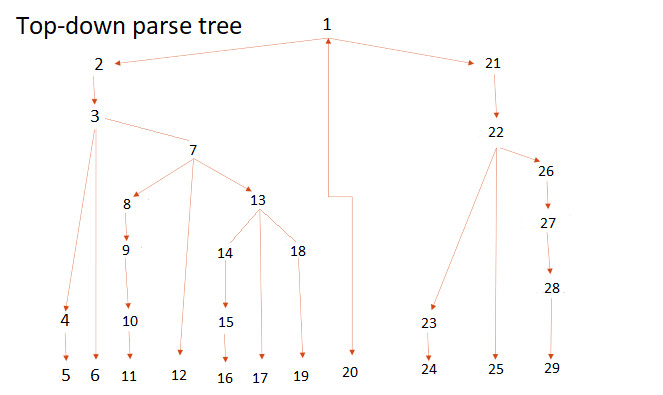
Figure 4: Top-down parse tree. Look at the numerical value and notice how it descends breaking the parse tree down, piece by piece.
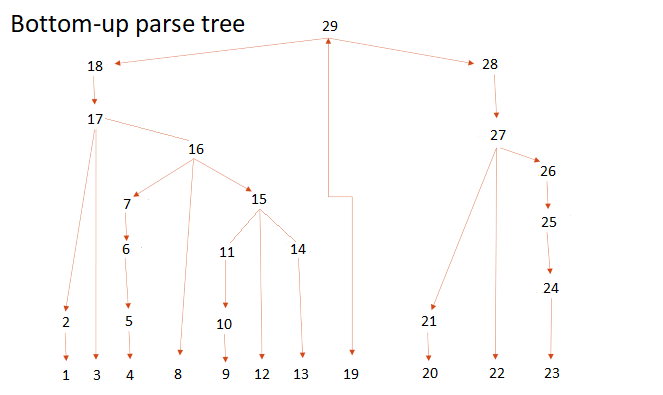
Figure 5: Notice how the bottom-up parse tree tries to compile all pieces from the bottom before it makes its way to the next tier. It is always building every piece to the root.
Example 3: Recursion and Bottom-up.
The Rod Cutting Problem is basic. There is n length of a rod. The seller is wanting to maximize profit. For each length of n there can be a price of i that can represent each length. The seller wants to know what the optimal price is. Should they cut the rod into pieces or sell the rod as it is.
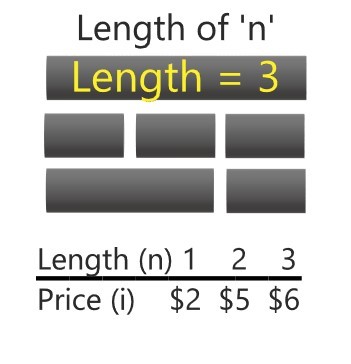
Figure 6: Rod Cutting Example
Example: Let’s say the seller has a rod with the length of 3. The price for length 1 is 2 dollars, length 2 is 5 dollars, and length 3 is 6 dollars.
If the seller wanted to cut the rod into 3 lengths of 1 then each rod would equal 2 dollars each making the profit 6 dollars. This would be equal to the price of the rod if it was not cut at all. If the seller were to cut the rod at a length of 1 and a length of 2, the seller can sell the rod at the price of 7 dollars instead of 6 dollars.
The rod at the length of 3 is very easy to compute, but as the bigger the rod gets in length the more complicated it becomes to solve. Therefore, it is imperative that in a dynamic program problem like the Rod Cutting Problem is optimized because if not it can drastically slow down the time complexity.
Below is an example of a recursive function.
import time start_time = time.time()